-
Property & Casualty
Property & Casualty Overview

Property & Casualty
We offer a full range of reinsurance products and the expertise of our talented reinsurance team.
Expertise
Publication
Structured Settlements – What They Are and Why They Matter
Publication
PFAS Awareness and Concern Continues to Grow. Will the Litigation it Generates Do Likewise?
Publication
“Weather” or Not to Use a Forensic Meteorologist in the Claims Process – It’s Not as Expensive as You Think
Publication
Phthalates – Why Now and Should We Be Worried?
Publication
The Hidden Costs of Convenience – The Impact of Food Delivery Apps on Auto Accidents
Publication
That’s a Robotaxi in Your Rear-View Mirror – What Does This Mean for Insurers? -
Life & Health
Life & Health Overview

Life & Health
We offer a full range of reinsurance products and the expertise of our talented reinsurance team.

Publication
Key Takeaways From Our U.S. Claims Fraud Survey
Publication
Favorite Findings – Behavioral Economics and Insurance
Publication
Individual Life Accelerated Underwriting – Highlights of 2024 U.S. Survey
Publication
Can a Low-Price Strategy be Successful in Today’s Competitive Medicare Supplement Market? U.S. Industry Events
U.S. Industry Events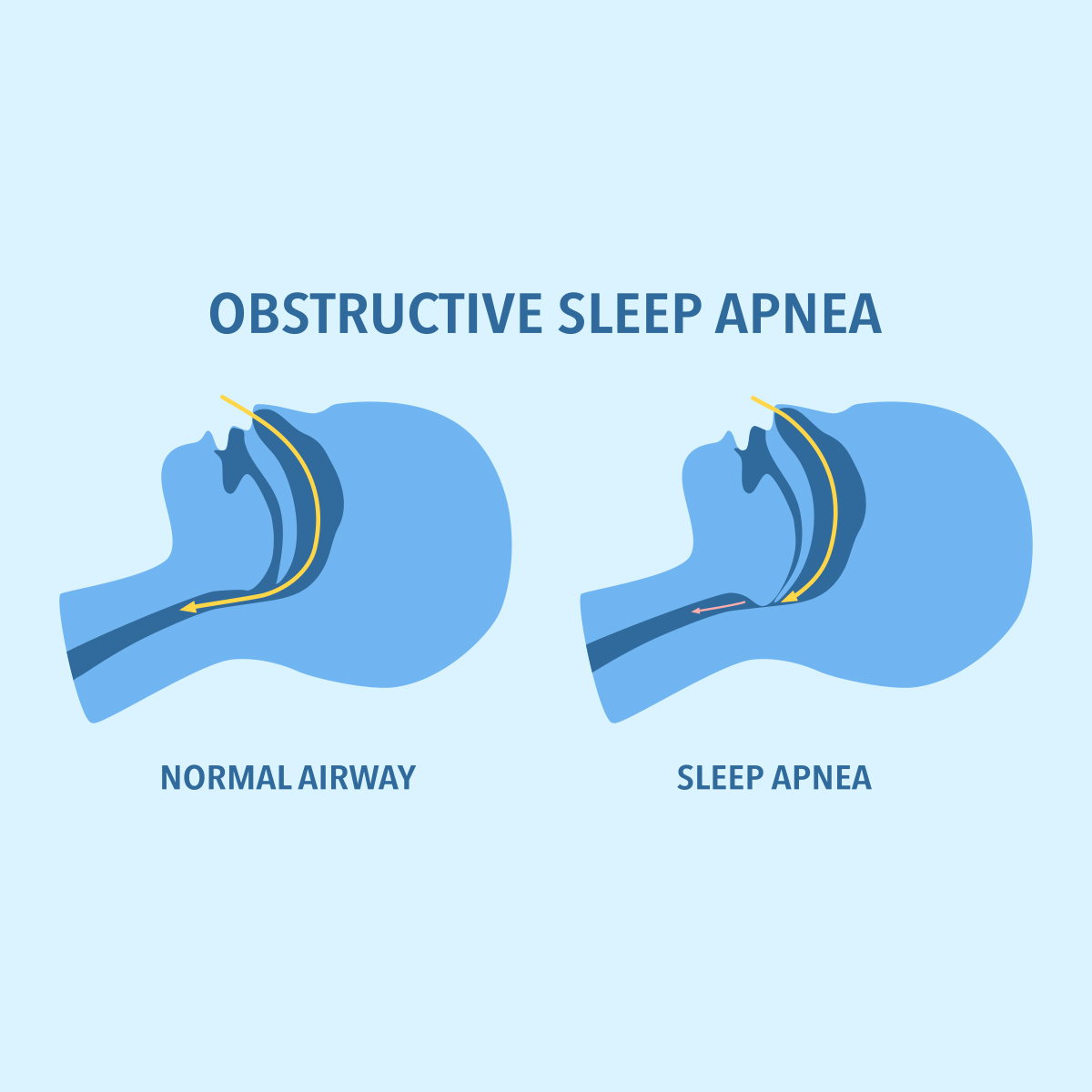
Publication
The Latest in Obstructive Sleep Apnea -
Knowledge Center
Knowledge Center Overview

Knowledge Center
Our global experts share their insights on insurance industry topics.
Trending Topics -
About Us
About Us OverviewCorporate Information

Meet Gen Re
Gen Re delivers reinsurance solutions to the Life & Health and Property & Casualty insurance industries.
- Careers Careers
The Future of Cryptography and the Rise of Quantum Computing

September 19, 2023
Frank Schmid
English
Deutsch
On August 21, 2023, three U.S. government agencies released a joint factsheet on quantum readiness titled Quantum-Readiness: Migration to Post-Quantum Cryptography. In this note, the Cybersecurity and Infrastructure Security Agency (CISA), the National Security Agency (NSA), and the National Institute of Standards and Technology (NIST) encourage organizations to develop a Quantum-Readiness roadmap for migration to post-quantum cryptographic standards.1
Quantum preparedness encompasses two aspects. The first aspect involves implementing post-quantum cryptography before quantum computers can successfully compromise classical cryptographic methods. The second aspect involves establishing post-quantum cryptography protocols prior to threat actors harvesting classically encrypted data with the intent to decrypt once quantum computers have acquired this capability.
This latter aspect, dubbed “harvest now, decrypt later”, is often regarded as more critical, especially for entities that store data with a long secrecy lifetime. Insurers and reinsurers who issue policies and agree to contracts covering long-term risks fall into this category.
Quantum Computing
Quantum computing is a paradigm of computing that leverages the principles of quantum mechanics to process and manipulate information. Unlike classical computers, which use bits as the smallest units of data represented as either 0 or 1, quantum computers use quantum bits, or qubits, which can exist in a superposition of states, representing both 0 and 1 simultaneously. This means that a set of two qubits can be in a superposition of four states, which therefore require four numbers to uniquely identify the state. More broadly, the amount of information stored in N qubits equals 2 raised to the power of N (2N) classical bits.
The principles of quantum mechanics enable quantum computing to perform certain types of calculations much faster than classical computing. Quantum computing achieves polynomial speedup if it solves a problem in time T for which a classical computer requires time T2 (for example) or some other polynomial function of T. Similarly, quantum computing achieves exponential speedup if it solves a problem in time T for which a classical computer takes time 2T (for example) or another exponentially growing function of T.2
Algorithms for quantum computing have been developed for combinatorial and optimization problems and certain types of simulations. Among the well-known quantum algorithms are Shor’s algorithm and Grover’s algorithm.
- Grover’s algorithm provides a quadratic speedup over classical algorithms in searching an unsorted database. It can find the desired item among N items in roughly the square root of N steps, compared to N steps classically. This algorithm has applications in database searching and optimization.
- Shor’s algorithm yields exponential speedup in determining the prime factors of numbers, a process referred to as factorization. This presents a challenge for classical cryptographic systems that rely on the practical difficulty of factoring large numbers to ensure security. This challenge extends to the widely adopted RSA protocol.3
Basic Principles of Quantum Computing
Qubits – The basic unit of information in quantum computing. Unlike classical bits, which can only be in one state at a time (0 or 1), qubits can exist in a superposition of two states. This means that a qubit can be both 0 and 1 at the same time.
Quantum entanglement – A phenomenon in which two qubits are linked together in such a way that they share the same fate. If one qubit is measured, the other qubit will instantaneously collapse into the same state, regardless of how far apart they are.
Quantum superposition – The ability of a qubit to exist in a superposition of two states. This allows quantum computers to perform calculations that are impossible for classical computers.
Quantum algorithms – The programs that run on quantum computers. Quantum algorithms are designed to take advantage of the unique properties of qubits.
Cryptography
Cryptography bifurcates into symmetric and asymmetric encryption methods. Symmetric encryption, also known as private-key encryption, uses a single key to both encrypt and decrypt data. This means that the same key is used to both scramble and unscramble the data, and the key must be kept secret to prevent unauthorized access. Examples of symmetric encryption algorithms include Advanced Encryption Standard (AES) and 3-DES (Triple Data Encryption Standard).
Asymmetric encryption, also known as public-key encryption, uses a pair of keys - a public key and a private key - to encrypt and decrypt data. The public key is freely available to anyone who needs to send encrypted data, while the private key is kept secret by the owner of the key pair. When someone wants to send encrypted data to the owner of the key pair, they use the owner’s public key to encrypt the data. The owner can then use its private key to decrypt the data. Examples of asymmetric encryption algorithms include RSA and Elliptic Curve Cryptography (ECC).4
Symmetric encryption is generally faster and more efficient than asymmetric encryption, but it requires a secure method for distributing the secret key. Asymmetric encryption, on the other hand, does not require a secure key distribution method, but it is generally slower and less efficient than symmetric encryption.
So, while RSA itself isn’t used for the bulk encryption of data due to its relatively slow speed compared to symmetric algorithms, it is heavily used for key exchange, that is securely exchanging the symmetric encryption keys that will be used for the actual data encryption and decryption. This combination of asymmetric and symmetric encryption provides both security and efficiency in secure communication.
Mechanics of Asymmetric Cryptography
Key generation – A user generates a pair of keys: a public key and a private key. These keys are linked in a way that data encrypted with one key can only be decrypted with the other key.
Public key distribution – The user shares its public key openly and widely. It’s called the public key because it’s not sensitive information and can be freely shared.
Encryption – If Alice wants to send a confidential message to Bob, Alice uses Bob’s public key to encrypt the message. Only Bob’s private key can decrypt this encrypted message.
Decryption – Bob, the recipient, uses its private key to decrypt the encrypted message received from Alice. The private key is kept secret and known only to Bob.
The security of asymmetric encryption relies on the fact that even though the public key is available to everyone, it’s computationally impracticable to derive the private key from the public key. This ensures that although anyone can encrypt messages using the recipient’s public key, only the recipient with the corresponding private key can decrypt these messages.
The Threat to Classical Cryptography
The threat of quantum computing to classical cryptography is largely confined to asymmetric encryption methods. Although Grover’s algorithm can break symmetric ciphers, it has been argued that increasing the key size can effectively fend off such attacks. Shor’s algorithm (and its variants), on the other hand, can solve all three hard-to-solve mathematical problems that current asymmetric encryption methods rely on for their security, one of which is prime factorization.5
RSA is the most prominent instance of an asymmetric encryption method using prime factorization. In simple language, the private key in the RSA encryption protocol is constructed using a pair of randomly selected prime numbers the product of which is a semiprime. The corresponding public key is derived from this semiprime. When transmitting a message, the sender employs the public key, acquired from the intended recipient, to perform the encryption. Upon receiving the encrypted message, the recipient employs the private key, generated from the primes, for decryption.
The RSA encryption key can be broken by factoring the semiprime, here denoted N, that is, by finding the (only) two prime numbers of which N is the product. For illustration, let’s assume N equals 35. Factorizing N is straightforward as it is immediately recognized as the product of 5 and 7, the (only) two prime numbers that generate the semiprime 35.
Modern implementations of RSA ciphers use prime numbers that are hundreds of digits in length. For instance, the RSA number of the 2048-bit RSA protocol that had been generated for the RSA Factoring Challenge launched in 1991 has 617 decimal digits. There is no known algorithm that allows classical computers to determine in a practical amount of time the prime factors of numbers that large.6 Nonetheless, Shor's algorithm, introduced in 1994, has demonstrated the capability to solve the factorization problem in polynomial time using quantum computing, thus providing the theoretical basis for breaking RSA.7
The implementation of Shor’s algorithm poses a formidable physical challenge. This is because today’s (physical) qubits are subject to errors, which are related to hardware limitations and noise from the surrounding environment.8 A 2019 experimental study of Shor’s factoring algorithm on an IBM Q quantum computer reports “excellent” performance in factoring the number 15 (3x5), whereas “deviations from the theoretical results become more noticeable” for 21 (3x7), and the factoring of the number 35 (5x7) failed due to accumulating errors.9 Remarkably, the semi-prime 35 is composed of just two decimal digits, a far cry from the 617 decimal-digit RSA number generated for the RSA Factoring Challenge using the 2048-bit protocol.
Although quantum computers have successfully factored larger numbers using alternative algorithms, these methods resemble classical brute-force methods for factor checking. Unlike Shor's algorithm, these approaches are not anticipated to surpass the performance of classical factorization algorithms.10
The breaking of a sufficiently strong RSA encryption key using Shor’s algorithm may be many years away.11 Large-scale quantum computing requires techniques that keep the errors generated by (physical) qubits from multiplying and spreading. Current error correction methods focus on the encoding of information into multiple physical qubits that are grouped into logical qubits.12
Post-Quantum Cryptography (PQC)
In 2016, National Institute of Standards and Technology (NIST) summoned the global community of cryptographers to create and assess encryption methods capable of resisting attacks from an advanced quantum computer, surpassing the power of today's limited machines. By 2022, NIST had selected the first set of encryption tools designed to withstand assaults from future quantum and classical computers alike. These four chosen encryption algorithms are on track to become integral to NIST’s post-quantum cryptographic standard, expected to be finalized by 2024.13
Notably, only one candidate has been put forth for key exchange, whereas the other three algorithms are digital signature schemes. The security of the public-key encryption algorithm CRYSTALS-Kyber is based on a hard-to-solve problem known as the shortest vector problem (SVP). Solving a large SVP instance to recover the private key is considered infeasible even for quantum computers.14
Conclusion
NIST suggests that over the next two decades, there is a plausible chance of quantum computers reaching a scale where they could potentially compromise all currently used public-key encryption methods. The joint factsheet on quantum readiness urges organizations to start preparing early by creating quantum-readiness roadmaps, conducting risk assessments, and engaging vendors. This is essential because data being targeted by threat actors today might still require protection in the future.
This blog was authored by Frank Schmid and reflects his thoughts; however, it was enhanced using Generative AI prior to Gen Re’s editorial and legal review.
- See Cybersecurity and Infrastructure Security Agency, “CISA, NSA, and NIST Publish Factsheet on Quantum Readiness,” August 21, 2023, https://www.cisa.gov/news-events/alerts/2023/08/21/cisa-nsa-and-nist-publish-factsheet-quantum-readiness.
- See Robin Kothari, “Quantum speedups for unstructured problems: Solving two twenty-year-old problems,” Microsoft Research Blog, May 4, 2020, https://www.microsoft.com/en-us/research/blog/quantum-speedups-for-unstructured-problems-solving-two-twenty-year-old-problems.
- The acronym RSA derives from the surnames of the algorithm’s creators, MIT researchers Ron Rivest, Adi Shamir, and Leonard Adleman, who introduced the algorithm in 1977.
- ECC hinges its security on the difficulty of finding the discrete logarithm of a random elliptic curve element with respect to a known base point. (See “Elliptic-curve cryptography,” Wikipedia, https://en.wikipedia.org/wiki/Elliptic-curve_cryptography.)
- Although the term Shor’s algorithm typically refers to the factoring of integers, this algorithm also solves the discrete logarithm problem and the elliptic-curve discrete logarithm problem. (See “Post-quantum cryptography,” Wikipedia, https://en.wikipedia.org/wiki/Post-quantum_cryptography.) It has been argued that that ECC is an easier target for quantum computers than RSA based on the quantum computing resources needed to compromise the protocol. (See “Elliptic-curve cryptography,” Wikipedia, https://en.wikipedia.org/wiki/Elliptic-curve_cryptography.)
- It has been posited that it will take a classical computer 300 trillion years to break an RSA 2048-bit encryption key. See QuintessenceLabs, “Breaking RSA Encryption – an Update on the State-of-the-Art,” June 13, 2019, https://www.quintessencelabs.com/blog/breaking-rsa-encryption-update-state-art.
- According to QuintessenceLabs, op. cit., a “quantum computer with 4099 perfectly stable qubits could break the RSA-2048 encryption in 10 seconds”. Note that a quantum computer with perfectly stable qubits is a theoretical construct.
- See IBM, The Quantum Decade, 3rd ed., November 2022, https://www.ibm.com/thought-leadership/institute-business-value/en-us/report/quantum-decade.
- See Mirko Amico et al., “An Experimental Study of Shor’s Factoring Algorithm on IBM Q,” May 14, 2019, https://arxiv.org/pdf/1903.00768.pdf.
- See “Shor’s algorithm,” Wikipedia, https://en.wikipedia.org/wiki/Shor%27s_algorithm.
- In 2021, the German mathematician Claus Peter Schnorr published an algorithm of which he claimed that it “destroys the RSA cryptosystems” using classical computing. (See “Fast Factoring Integers by SVP Algorithms, corrected,” https://eprint.iacr.org/2021/933.pdf). It then turned out that this algorithm lacks scalability, a challenge that Chinese researchers in December 2022 claimed to have overcome using quantum computing. (See Bao Yan et al, “Factoring integers with sublinear resources on a superconducting quantum processor,” https://arxiv.org/pdf/2212.12372.pdf.) The Financial Times reports Peter Shor commenting that “[a]s far as I can tell the paper is not wrong” but that the Chinese researchers had “failed to address how fast the algorithm will run”. Shor continued that it was possible that it “will still take millions of years” and concluded that “[i]n the absence of any analysis showing that it will be faster, I suspect that the most likely scenario is that it’s not much of an improvement.” (See Financial Times, January 4, 2023, “Chinese researchers claim to find way to break encryption using quantum computers,” https://www.ft.com/content/b15680c0-cf31-448d-9eb6-b30426c29b8b.)
- See Sundar Pichai, February 22, 2023, “Our progress toward quantum error correction.” https://blog.google/inside-google/message-ceo/our-progress-toward-quantum-error-correction.
- See NIST, July 5, 2022, “NIST Announces First Four Quantum-Resistant Cryptographic Algorithms,” https://www.nist.gov/news-events/news/2022/07/nist-announces-first-four-quantum-resistant-cryptographic-algorithms.
- For a gentle introduction to Kyber, see Ruben Gonzales, September 14, 2021, “Kyber – How does it work?”, https://cryptopedia.dev/posts/kyber.





